Anforderungen an die Siebung
Wie viel Siebung soll nun sein und wie wird das berechnet? Oder präziser ausgedrückt: um wieviel müssen Wechselspannungsreste auf der Versorgungs-Gleichspannung gedämpft werden? Dazu müssen wir uns zunächst einmal mit der Angabe von Spannungsverhältnissen beschäftigen. Diese werden in Dezibel (dB) angegeben. Ohne das im Einzelnen herleiten zu wollen, sei das Folgende dazu gesagt:
Ein Spannungsverhältnis von
- 1:1 entspricht 0dB
- 10:1 entspricht dem Wert 20 dB
Beispiel: man stelle sich vor, man schicke in eine black box 10Volt Spannung hinein und erhalte am Ausgang lediglich 1Volt, dann erfährt die Eingangsspannung eine Dämpfung von -20dB. Umgekehrt: schickt man eine Spannung von 1Volt in eine black box hinein und erhält an deren Ausgang 10Volt, findet eine Verstärkung von +20dB statt. - 100:1 entspricht 40dB
- 1000:1 entspricht 60dB
- 10000:1 entspricht 80dB
- …
Die Spannungsverhältnisse stehen in logarithmischem Zusammenhang mit dem entsprechenden dB-Wert, dabei gibt es natürlich alle Zwischenwerte. (Anmerkung: hier geht es ausdrücklich um Spannungsverhältnisse!)
Spannungsverhältnisse werden multipliziert, ihre dB-Werte addiert. Beispiel:
einem Dämpfungsglied mit einem Dämpfungsfaktor von 100:1 wird ein gleiches nachgeschaltet. Eine am Eingang eingespeiste Spannung wird dann zwei Mal um den Faktor 100 vermindert:
100:1 mal 100:1 = 10.000:1
in dB ausgedrückt: -(40dB plus 40dB) = -80dB
Nun zu den Anforderungen an die Dämpfung der Störsignale auf der Versorgungsspannung. Freund Segschneider schreibt dazu:
In der idealen Welt ist der Gleichstrom unendlich gleich, er kennt keine Welligkeiten. Leider leben wir in der Wirklichkeit, und die ist oft alles andere als ideal. Wie groß dürfen die Verunreinigungen des Gleichstroms sein, das ist die entscheidende Frage. Glücklicherweise ist sie leicht zu beantworten. Wir müssen lediglich das Denken in Röhren beiseiteschieben und über aufgenommene Musik nachdenken. Gute Aufnahmen, ob nun auf CD oder auf LP, speichern circa 60db Signal (Anm. MiMü: nach obiger Aufstellung ist also die größte Signalspannung 1000 x so groß wie die kleinste Signalspannung). Das wurde mehrfach durch Messungen bestätigt. Ziehen wir darüber hinaus in Betracht, wie Menschen hören (können), dann müssen wir berücksichtigen, dass das menschliche Ohr Signale erkennt, die – sehr behutsam formuliert – gute 20db unterhalb des Rauschpegels liegen. Auch das ist vielfach bestätigt, freilich nicht durch Messen (bis heute können die Techniker da nichts messen), sondern durch Hören. Und da wir ja für MusikHÖRER konstruieren, nehmen wir das ernst.
Fassen wir diese erste Betrachtung zusammen, ergibt sich folgendes Bild: würden wir die Störsignale auf dem Gleichstrom, seien sie nun Restwelligkeiten oder andere Unregelmäßigkeiten, um 60db + 20db = 80db vermindern, dann wäre das Störsignal noch genauso laut wie das kleinste Musiksignal. Die Störsignale würden sich mit den Musiksignalen 1:1 mischen und natürlich auch miteinander intermodulieren. Das kann nicht wünschenswert sein.
Wollen wir also, dass die Störsignale – ähnlich wie der Klirr – mindestens 40db leiser sein sollen als das kleinste Musiksignal (40db entsprechen einem Klirr von 1%), kommen wir zu der (harten!) Forderung, dass unser Netzteil 80db plus weitere 40db, insgesamt also 120db Dämpfung und Welligkeitsunterdrückung leisten muss!
Die obige Aufzählung weiterdenkend finden wir, dass -120dB einem Spannungsverhältnis von 1.000.000:1 entsprechen. Das bedeutet, das Störsignal beträgt nur noch ein Millionstel des größten Signalpegels. Man kann es auch so ausdrücken: wir brauchen ein Netzteil mit einem Siebfaktor von 1.000.000 (1:1 Million). Die Dämpfung des Störsignals beträgt dann -120dB.
Kritische Naturen mögen nun einwenden, hier würden Äpfel mit Birnen verglichen. Man könne doch wohl die größte vorkommende Nutzsignalspannung nicht mit der ungedämpften Welligkeit der gleichgerichteten Anodenspannung vergleichen. Das geht allerdings ohne weiteres. Zur Erklärung hier noch mal eine Abbildung, die schon weiter oben zum Einsatz kam:

Dabei handelt es sich um die Dauertest-Schaltung des Netztrafos. Gerade habe ich den in der Abbildung beschriebenen Testfall noch einmal hergestellt. Diesmal aber habe ich zusätzlich mit dem Oszilloskop die Welligkeit der Gleichspannung am Ladeelko (220µF) gemessen. Die Gleichspannung selbst beträgt 275V, deren Welligkeit liegt bei lediglich 3Vss, das entspricht etwa 1Veff und liegt somit durchaus im Bereich des maximalen Eingangssignals der Endstufe. Dieses eine Volt ist es auch, das in der noch zu errechnenden Siebkette um 120dB gedämpft werden soll.
Gleichrichtung, RC-Glieder und Siebkette
Gleichrichtung
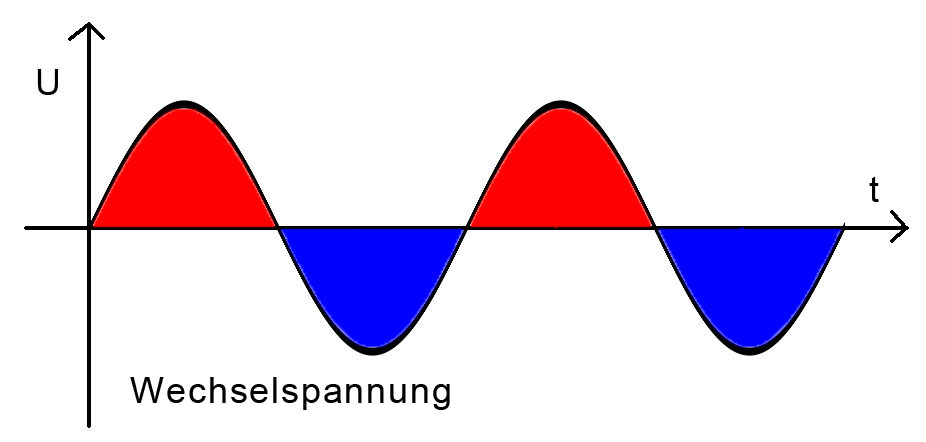
Untersuchen wir nun, was der Gleichrichter macht und was das für die danach zu besprechende Siebkette bedeutet. Zunächst sehen wir uns eine Wechselspannung an, so wie sie aus der Sekundärwicklung unseres Netztrafos kommt. Jeweils eine positive (rot) und eine negative (blau) Halbwelle ergeben eine volle Schwingung, die Anzahl der Schwingungen pro Sekunde wird in Hertz (Hz) angegeben. Unsere Netzwechselspannung vollführt in einer Sekunde 50 Schwingungen, hat also die Frequenz von 50 Hz:
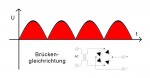
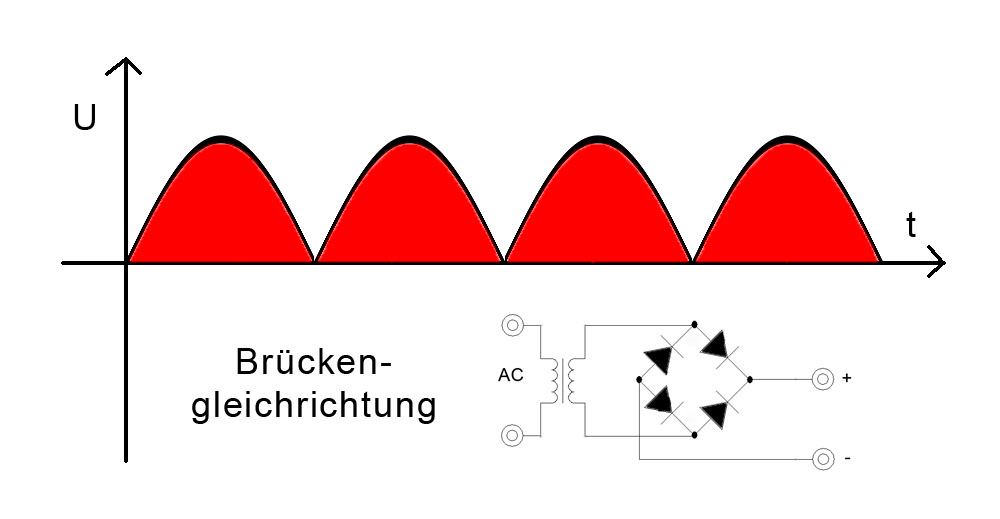
Der Brückengleichrichter unterdrückt nun die negativen Halbwellen und führt die an den beiden Trafoanschlüssen gegenphasig auftretenden positiven Halbwellen zusammen auf einen Punkt. Im Oszillogramm sieht das so aus, als würden die negativen Halbwellen gleichsam „nach oben geklappt“:
Am Oszillogramm sieht man auch, dass die Welligkeit der entstandenen pulsierenden Gleichspannung die doppelte Frequenz der zugeführten Wechselspannung hat, aus der Netzfrequenz von 50Hz ist ein „ripple“ mit der Frequenz von 100Hz geworden. Wie wir später noch sehen werden, kommt uns das sehr zupass, da dies den Aufwand bei der Siebung der Gleichspannung für unseren Röhrenverstärker „halbiert“.
RC-Glieder und Siebkette
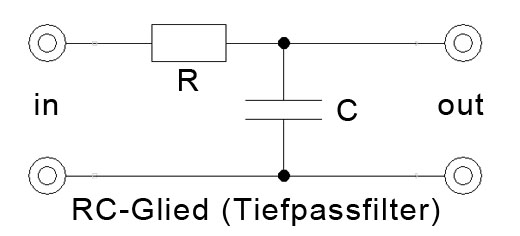
Ich habe mich bei meinen Netzteilen für den Einsatz von RC-Gliedern entschieden. Ein RC-Glied sieht folgendermaßen aus:
Es handelt sich hierbei um ein Tiefpassfilter, d.h. es lässt bevorzugt Spannungen von tiefer Frequenz durch und dämpft Spannungen höherer Frequenz. Gleichspannungen werden unverändert durchgelassen. Wie stark die Spannung einer bestimmten Frequenz bedämpft wird, lässt sich in einer Formel fassen. Es gilt:
S = 2π * f * R * C
S = Siebfaktor
π = Kreiszahl = 3,14
f = Frequenz (in Hz)
R = Widerstand (in Ω)
C = Kapazität (in F)
Beispiel: unser zu dämpfender Wechselspannungsanteil hat eine Frequenz von 100Hz, der Widerstand sei 330Ω und der Kondensator 470µF. Dann beträgt der Siebfaktor
S = 2 * 3,14 * 100Hz * 330Ω * 0,00047 F = 97,4 (ohne Einheit!)
Der Siebfaktor S ist gleich dem Spannungsverhältnis der Wechselspannung am Eingang des RC-Glieds zur Wechselspannung an dessen Ausgang. In unserem Beispiel ergibt sich ein Spannungsverhältnis von 97,4:1. Das entspricht einer Dämpfung von -39,8dB. Das ist noch weit entfernt von den weiter oben geforderten 120dB für die Versorgung der Endröhre. Was tun?
Glückes Geschick, tirili! RC-Glieder lassen sich hintereinander schalten! Wir rechnen mal: zwei der eben berechneten RC-Glieder hintereinander haben bei 100Hz einen Siebfaktor von 97,4 * 97,4 = 9487. Nun haben wir ein Spannungsverhältnis von 9487:1 entsprechend einer Dämpfung von -79,6dB – das kommt unserem Ziel schon näher!
Da wir wissen, dass man in dB ausgedrückte Spannungsverhältnisse addiert, fügen wir unserer Siebkette (eine solche tüfteln wir hier gerade zusammen!) ein weiteres RC-Glied hinzu, indem wir noch einmal -39,8db hinzuzählen und kommen auf insgesamt -119,4dB Dämpfung. Hey – beinah Punktlandung! Das könnte man nun schon so lassen. Es gibt den ein oder anderen Grund, unsere Siebkette noch zu modifizieren. Davon später mehr …
Anmerkung: weiter oben wurde behauptet, dass das der Gleichspannung aufgeprägte Störsignal wegen seiner gegenüber der 50Hz-Netzspannung verdoppelten Frequenz von 100Hz halb so viel Aufwand bei der Siebung verursache. Dass das stimmt, sehen wir, wenn wir in unsere Gleichung bei sonst unveränderten Werten als Frequenz 50Hz einsetzen:
S = 2 * 3,14 * 50Hz * 330Ω * 0,00047 F = 48,7 (ohne Einheit!)
Tatsächlich ist der Siebfaktor nur noch halb so groß!
Wichtiger Link zu diesem Abschnitt: der dB-Rechner auf den Seiten von Sengpiel Audio!
Spannungsabfall in der Siebkette
Wir haben gerade eine Siebkette gebildet aus drei Widerständen von je 330Ω und drei Kondensatoren von je 470µF. Das Netzteil sieht nun inklusive Gleichrichter und Ladelko so aus:
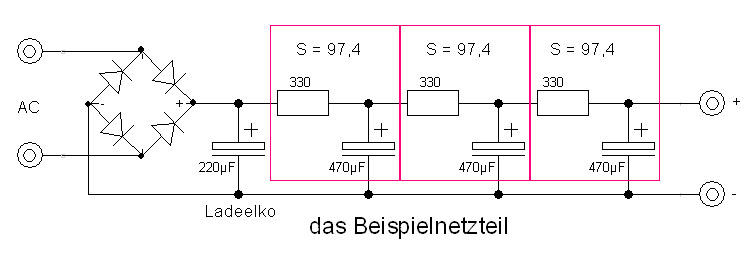
Wir stellen uns jetzt vor, die zu versorgende Endröhre ließe einen Strom von 44mA fließen. O je, der fließt dann ja auch durch die in Reihe liegenden Längswiderstände in der Siebkette und ruft dort einen Spannungsabfall hervor! Der berechnet sich zu
U = R * I = 990Ω * 0,044A = 43,56V
Nur mal angenommen, die Einspeisespannung in den Endröhrenkreis soll 250V betragen. Dann muss der Trafo in der Lage sein, nach Gleichrichtung am Ladeelko eine Gleichspannung von 250 + 43,6 = 293,6V, also rund 295V zur Verfügung zu stellen! Und für den Trafo kommt es noch dicker: Es gibt ja noch einen zweiten Verstärkerkanal und je Kanal eine Vorstufenröhre und jede Röhre bekommt eine eigene Siebkette. Bei einem Vorröhrenstrom von sagen wir 4mA und dem der Endröhre von 44mA kommen wir auf eine Gesamt-Stromaufnahme einer gedachten Stereo-Endstufe von 2 * 4mA + 2 * 44mA = 96mA. Die Anforderung an den Trafo lautet also, bei einer Stromaufnahme der Endstufe von 96mA am Ladeelko um die 295Volt zu liefern. Das ist schon was!
Kleine garstige Bemerkung: wir ahnen, dass es keinen Sinn macht, eine Endstufe um einen zufällig vorhandenen Netztrafo herum zu stricken. Umgekehrt wird ein Schuh draus: die Endstufe gibt vor, was der Trafo zu leisten hat! Das macht in der heutigen Zeit, in der es kaum noch auf Bastler eingestellte Trafowickelbetriebe gibt, den Selbstbau von Röhrenendstufen nicht gerade leichter. Wohl dem, der über eine gut gefüllte Bastelkiste verfügt – vielleicht schlummert ja dort der passende Trafo …
Wie viele RC-Glieder kann man sinnvoll hintereinander schalten?
Man stelle sich drei hintereinander geschaltete RC-Glieder vor, die bei der Frequenz 100Hz einen Siebfaktor von je 100 haben. Der gesamte Siebfaktor beträgt 100*100*100 = 1.000.000. Bei einer Frequenz von 50Hz beträgt der Siebfaktor des einzelnen RC-Glieds lediglich noch 50, der gesamte Siebfaktor ist 50*50*50 = 125.000. Das ist nur noch ein Achtel des Werts bei 100Hz.
Eine Siebkette mit dem Siebfaktor 1.000.000 bei 100Hz kann man natürlich auch mit vier RC-Gliedern aufbauen, die jeweils einen Siebfaktor von ca. 32 haben: 32*32*32*32 = 1.048.576. Bei 50Hz sinkt der Siebfaktor des einzelnen RC-Glieds auf 16. 16*16*16*16 = 65.536. Das ist ein Verhältnis von 1.048.576 / 65.536 = 16, also lediglich noch ein Sechszehntel des Werts bei 100Hz.
Es ist also besser, sich auf drei RC-Glieder zu beschränken, um die Dämpfung im Bereich der tieferen Frequenzen nicht zu gering werden zu lassen.