Resonanzverhältnisse
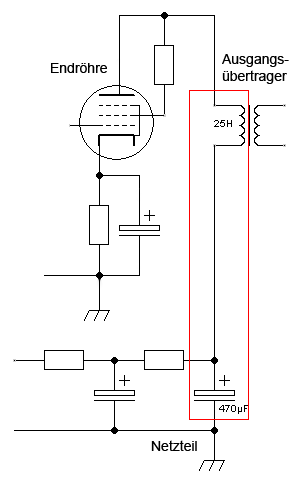 Betrachten wir einmal den nebenstehenden Schaltplanauszug. Er zeigt eine als Triode beschaltete Endpentode, den Ausgangstrafo und die Anbindung an das Netzteil (unten). Und wenn man mal genauer hinguckt – auch ich musste mit der Nase drauf gestoßen werden – erkennt man unschwer einen Serienschwingkreis (rot eingerahmt), gebildet aus dem letzten Kondensator des Netzteils (470µF) und der Induktivität der Primärwicklung des Ausgangsübertragers (hier angenommen mit 25H, was ein für gängige Trafos durchaus plausibler Wert ist). Die Resonanzfrequenz dieses Schwingkreises berechnet sich zu:
Betrachten wir einmal den nebenstehenden Schaltplanauszug. Er zeigt eine als Triode beschaltete Endpentode, den Ausgangstrafo und die Anbindung an das Netzteil (unten). Und wenn man mal genauer hinguckt – auch ich musste mit der Nase drauf gestoßen werden – erkennt man unschwer einen Serienschwingkreis (rot eingerahmt), gebildet aus dem letzten Kondensator des Netzteils (470µF) und der Induktivität der Primärwicklung des Ausgangsübertragers (hier angenommen mit 25H, was ein für gängige Trafos durchaus plausibler Wert ist). Die Resonanzfrequenz dieses Schwingkreises berechnet sich zu:
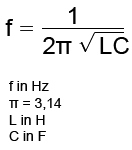
Ach, ich bin ein fauler Kerl und mag mich nicht mit irgendwelchen kompliziert zu bedienenden Programmen zur Darstellung von mathematischen Gleichungen befassen. Man verzeihe mir also meine Sauklaue, wenn ich nun rechne:
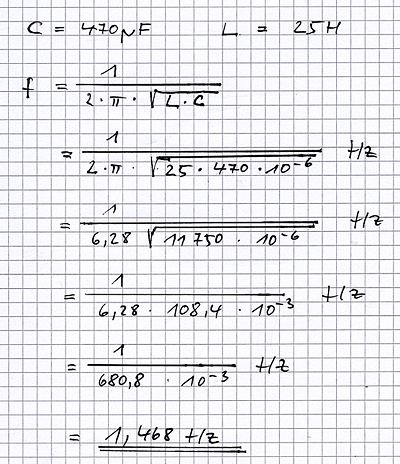
Was passiert da? Nun, das vom Verstärker übertragene Frequenzgemisch gibt unserem Resonator mal hier, mal da einen passenden Stups – fast so wie ein Vater, der sein Kind auf der Schaukel anschiebt. Um mal bei der Schaukelanalogie zu bleiben: wenn nicht nur der Vater anschiebt, sondern auch noch die Mutter, die gegenüber steht, vielleicht auch noch Onkel und Tante, die gelegentlich im passenden Moment von der Seite ein bisschen nachhelfen, dann bleibt die Schaukel in Bewegung. Die Erwachsenen können die Schaukel aber anstupsen, so oft sie wollen: die Schwingungsdauer der Schaukel bleibt konstant, genau wie die Resonanzfrequenz von Ausgangstrafo und Netzteilelko in dem oben beschriebenen Beispiel. Also: es entsteht eine Schwingung mit der Frequenz 1,468Hz.
Die liegt aber weit unterhalb des Übertragungsbereichs. Welchen Schaden richtet die überhaupt an?
Mal sehen, was Segschneider dazu sagt:
„Was ist Intermodulation? Die Messgerätefirma Bruel & Kjaer hat’s 1977 klar gemacht mit folgendem Beispiel. Ein Tonarm habe eine Resonanz von 7Hz (also unterhalb des Übertragungsbereichs!) und ich taste per Messschallplatte nun 1kHz ab, dann entstehen 993Hz, 1kHz und 1007Hz (und die sind NICHT unterhalb der Hörschwelle) – der erste und letzte Wert sind um so kleiner, je kleiner die Güte des Schwingkreises ist.“
Das ist wohl einzusehen: in unserem berechneten Fall heißt das, dass aus einem 1kHz-Signal drei Signale werden: das recht starke 1kHz-Signal selbst, ein unteres Seitenband von 998,5 Hz und das obere Seitenband von 1001,5 Hz.
Noch was Neues, die Güte des Schwingkreises! Was ist das? Die Güte Q ist ein Maß dafür, wie stark die resonanten Schwingungen im Kreis selbst gedämpft werden. Der Verursacher der Dämpfung in unserem Beispiel-Schwingkreis ist schnell ausgemacht: es ist der bisher noch nicht erwähnte Kupferwiderstand der Primärwicklung des Ausgangstrafos. Wir bedienen uns in der einschlägigen Literatur und finden diese Formel:
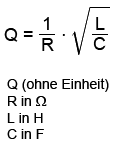
Wir setzen die uns bekannten Werte ein: L=25H, C=470µF und R=550 Ohm und erhalten:
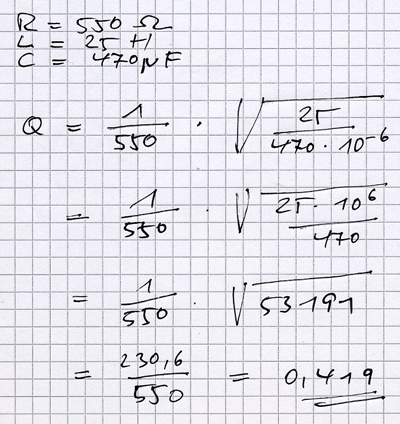
Q=0,419 ist für unsere Sache ein guter Wert, wie wir gleich sehen werden. In der Physik gibt es abhängig von der Güte drei Fälle:
- die Güte ist größer als 0,5: die Dämpfung im schwingungsfähigen System ist so schwach, dass sich Schwingungen ausbilden können, dieser Status nennt sich Schwingfall
- die Güte ist gleich 0,5: die Dämpfung im schwingungsfähigen System ist so groß, dass gerade keine Schwingungen mehr auftreten, man nennt das den aperiodischen Grenzfall
- die Güte ist kleiner als 0,5: die Dämpfung im schwingungsfähigen System ist so stark, dass keine Schwingungen auftreten können, das ist der Kriechfall oder auch ein Fall von überkritischer Dämpfung
Na prima, unsere Kreisgüte beträgt lediglich 0,419 und liegt damit unter 0,5. Das minimiert natürlich auch die unerwünschten Intermodulationsprodukte!
Segschneider hat’s schon gewusst. Hätte ich’s mal gleich gelesen:
Segschneider:
„Wenn wir also ca 1,5Hz als Resonanz haben, sind wir schon besser dran als mit zum Beispiel 10Hz, denn bei 10Hz würden wir bei einer Nutzfrequenz von 20Hz beispielsweise 10Hz und 30Hz als Seitenbänder bekommen, das gäbe schlimme Aufschaukelungen! Und noch besser sind wir mit der Güte von 0,419 dran, denn allgemein gilt ein Wert von 0,5 als die Grenze des Kritischen, darunter ist anzustreben und sehr gut.“
Na also – geht doch!
Leistungsanpassung
Für die folgenden Überlegungen soll eine als Triode geschaltete Endpentode PL82 als Beispiel dienen. Wie den Röhrenkennlinien (nach Tom Schlangen) zu entnehmen ist, fließt bei einer Anodenspannung von 205 Volt und einer Gittervorspannung von -16Volt ein Anodenstrom von 44mA durch die Röhre. Ihr Gleichstrom-Innenwiderstand bemisst sich demzufolge unter diesen Bedingungen zu R=U/I = 205V/0,044A = 4659 Ohm.
Ebenso wichtig für uns: der Wechselstrom-Innenwiderstand der Röhre. Verändert man bei gleichbleibender Gittervorspannung die Anodenspannung, so ändert sich auch der Anodenstrom. Der Quotient der Änderung der Anodenspannung und der Änderung des Anodenstroms ergibt den Wechselstromwiderstand der Röhre. Bei der PL82 liegt dieser zwischen 900 und 1000 Ohm. Man kann ihn den Röhrenkennlinien entnehmen. Oder man rechnet ihn aus, wenn man die Verstärkung der Röhre und ihre Steilheit kennt. Das sind aber ebenfalls Werte, die man den Kennlinien entnimmt.
Überhaupt darf man eine Röhre nicht mit einem rein ohmschen Widerstand vergleichen, dessen Verhalten komplett berechenbar wäre. Eine Röhre liefert ein lediglich in Grenzen und nur auf einen jeweiligen Betriebsfall hin berechenbares, im Ganzen aber nichtlineares Verhalten, das von Spannungen und Strömen, vor allem aber von ihren gekrümmten Kennlinien bestimmt ist.
Es ist sinnvoll, die Summe der Längswiderstände in der Siebkette des Netzteils in etwa nach dem Wert des Wechselstromwiderstandes der Röhre zu bemessen.
Lassen wir wieder Segschneider zu Wort kommen:
(…) es geht ja wesentlich darum, sicher zu stellen, dass sich das Netzteil und die Röhre in der Nähe des Arbeitspunktes gleich verhalten, dass ihre potentiellen Veränderungen gleich sind. Das ist Anpassung. (…)
(…) es geht nur um die Übereinstimmung im elektrischen Verhalten von Röhre – gegeben durch das Röhrendiagramm – und Netzteil – gegeben durch dessen Längswiderstand.
Siebkette der Vorröhre
Im zweiten Teil der Beitragsserie über das Netzteil fanden wir, dass unser Trafo bei einer Belastung von 96mA am Ladeelko eine Gleichspannung von 295Volt zur Verfügung stellen muss. 96mA sind die Summe von 2x44mA für die zwei Endröhren und 2x4mA für die Vorröhren unserer Endstufe. Eine Vorröhre zieht also 4mA und das bei einer Spannung von 260Volt. 295V-260V=35V – das ist der Spannungsüberhang, der bei einem Strom von 4mA an den Längswiderständen einer Vorröhren-Siebkette abfällt. Der Gesamtwiderstand berechnet sich zu R=U/I = 35V/0,004A = 8750 Ohm. Auf drei Widerstände verteilt könnte das so aussehen: 2,7kOhm + 2,7kOhm + 3,3kOhm = 8,7kOhm (die fehlenden 50 Ohm liegen im Bereich der Fertigungstoleranzen der Widerstände).
Ein RC-Glied mit einem Widerstand von 2,7kOhm und einem Elektrolytkondensator von 100µF hat einen Siebfaktor von 170. Ein gleiches RC-Glied nachgeschaltet ergibt zusammen mit dem ersten einen Siebfaktor von 28.900. Das dritte RC-Glied soll nun so bemessen sein, dass sich zusammen mit den beiden anderen ein Siebfaktor von besser 10.000.000 ergibt, das entspräche dann einer Dämpfung von -140dB oder besser. Wir rechnen: 10.000.000/28.900 = 346, das muss der Siebfaktor des letzten RC-Glieds sein. Frequenz (100Hz) und Widerstand (3,3kOhm) stehen fest, also lösen wir die schon bekannte Siebfaktor-Gleichung zum Kondensator hin auf:
C = 346/(2*3,14*100*3300) = 346/2.072.400 = 0,000167F = 167µF
Wir nehmen einen Kondensator von 220µF, der nun tatsächlich zu einem Siebfaktor von 456 führt, zusammen mit den beiden ersten RC-Gliedern ergibt sich ein Siebfaktor von 13.178.400, was einer Dämpfung von -142dB entspricht.