Auflistung aller Beiträge zum Thema (älteste zuerst)

Netzteil für einen Röhrenverstärker #1
Vorwort Nachfolgend beschreibe ich den Aufbau einer höchstwertigen, RC-gesiebten Spannungsversorgung für einen Röhrenverstärker mit der PL82 als End- und der PC86 als Vorröhre. Im Zusammenhang mit der von Wilimzig/Gysemberg veröffentlichten ...
Weiterlesen …
Weiterlesen …
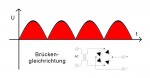
Netzteil für einen Röhrenverstärker #2
Anforderungen an die Siebung Wie viel Siebung soll nun sein und wie wird das berechnet? Oder präziser ausgedrückt: um wieviel müssen Wechselspannungsreste auf der Versorgungs-Gleichspannung gedämpft werden? Dazu müssen wir ...
Weiterlesen …
Weiterlesen …
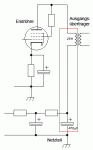
Netzteil für einen Röhrenverstärker #3
Resonanzverhältnisse Betrachten wir einmal den nebenstehenden Schaltplanauszug. Er zeigt eine als Triode beschaltete Endpentode, den Ausgangstrafo und die Anbindung an das Netzteil (unten). Und wenn man mal genauer hinguckt - ...
Weiterlesen …
Weiterlesen …

Netzteil für einen Röhrenverstärker #4, praktische Ausführung
Praktische Ausführung eines Netzteils Vorbemerkung: Die nachfolgend gemachten Angaben beziehen sich einerseits auf eine zu versorgende Endstufenschaltung mit konkreten Betriebswerten, andererseits aber auf die Verwendung eines Netztrafos, der "zufällig" in ...
Weiterlesen …
Weiterlesen …
